光照模型

几种光照模型有什么不同

进入摄像机光线的四个部分

• 自发光部分（emissive）

• 高光反射部分（specular）

• 漫反射（diffuse）

• 环境光（ambient）

逐像素与逐顶点

在片元着色器中计算，即逐像素光照，在顶点着色器中计算，即逐顶点光照。

• 在逐像素光照中，以每个像素为基础，对顶点法线进行插值（也可以从法线纹理中采样）得到它的法线，这种在面片之间对顶点法线进行插值的技术也被称为Phong着色（不同于Phong光照模型）。

• 逐顶点光照，也被称为高洛德着色（Gouraud shading），在逐顶点光照中，计算每个顶点上的光照，然后在渲染图元内部进行线性插值，最后输出成像素颜色。由于顶点数目往往远小于像素数目，所以计算量很小。但是，逐顶点光照依赖于线性插值，当光照模型的计算有非线性的计算（例如计算高光反射）时，逐顶点光照就会出现问题，渲染图元内部的颜色总会暗于顶点处的最高颜色值（通过插值计算得到的），某些情况下会导致非常明显的棱角现象。

漫反射光照模型

兰伯特光照模型公式：

$$c_{\text {diffuse }}=(c_{\text {light }} \cdot m_{\text {diffuse }}) \max (0, \hat{n} \cdot \hat{l})$$

半兰伯特光照模型，为了解决兰伯特光照模型背光面的明暗一致问题，Valve在开发游戏《半条命》时提出的一种技术，公式如下：

$$c_{\text {diffuse}}=(c_{\text {light}} \cdot m_{\text {diffuse}})(\alpha (\hat{n}\cdot\hat{l})+\beta)$$

半兰伯特模型对$\hat{n}\cdot\hat{l}$进行了一个$\alpha$倍的缩放和一个$\beta$大小的偏移，一般$\alpha$和$\beta$都取0.5，公式也就变成：

$$c_{\text {diffuse}}=(c_{\text {light}} \cdot m_{\text {diffuse}})(0.5 (\hat{n}\cdot\hat{l})+0.5)$$

可以看出，不同的地方就是用什么方法将$[-1,1]$映射到$[0,1]$，在半兰伯特模型中，负值不是直接映射为0，而是映射到$[0,0.5]$（取决于你的参数），从而使得背光面也有明暗变化。

需要注意的是，半兰伯特是没有任何物理依据的，它仅仅是一个视觉增强技术。

高光反射光照模型

Phong光照模型

Phong光照模型非常的直观，反射后的光线会进入眼睛，我们只需要计算反射方向与视角方向的夹角就可以得知反射光有多少光线进入眼睛。

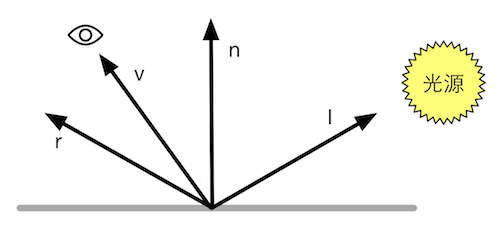
高光反射部分的计算公式：

$$c_{\text{specular}}=(c_{\text{light}}\cdot m_{\text{specular}}){\max(0, \hat{v}\cdot\hat{r})}^{m_{\text{gloss}}}$$

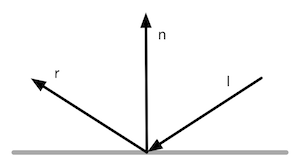
从公式可以看出，高光反射的计算需要四个四个参数：入射光线的颜色和强度$c_{\text{light}}$，材质的高光反射系数$m_{\text{specular}}$，视角方向$\hat{v}$以及反射方向$\hat{r}$。其中，反射方向可以由表面法线$\hat{n}$和光源方向$\hat{l}$计算而得：

$$\hat{r}=\hat{l}-2(\hat{n}\cdot\hat{l})\hat{n}$$

上述公式非常简单，甚至在Unity Shader和OpenGL中，都有reflect函数可以直接使用。

Blinn-Phong光照模型

Blinn-Phong光照模型稍微有一点绕，它避免了计算反射方向$\hat{r}$，你可以想象你在你的头上举一个手电筒，打在一面镜子上，当镜子朝向你的眼睛和手电筒连线的中点时，那么反射出来的光线会正好照在你的眼睛里，因此我们只需要计算朝向中点的方向与镜子朝向的角度（即法向）的夹角即可。

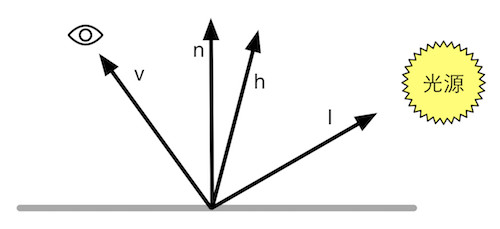
Blinn模型引入了一个新的向量$\hat{h}$（代码中一般的命名是halfDir），它是由视角方向$\hat{v}$和光源方向$\hat{l}$取平均后再归一化得到的：

$$\hat{h}=\frac{\hat{v}+\hat{l}}{|\hat{v}+\hat{l}|}$$

然后，使用$\hat{n}$和$\hat{h}$之间的夹角进行计算，公式如下：

$$c_{\text{specular}}=(c_{\text{light}}\cdot m_{\text{specular}}){\max(0, \hat{n}\cdot\hat{h})}^{m_{\text{gloss}}}$$

两种光照模型的对比

当摄像机和光源距离模型足够远时，Blinn模型会快于Phong模型，因为可以认为$\hat{v}$和$\hat{l}$为定值，则$\hat{h}$将会是一个常量。但是当$\hat{v}$和$\hat{l}$不为定值时，Phong模型可能反而会更快一些。需要注意的是，两者都是经验模型，我们不应该认为Phong模型更加的正确，实际上在一些情况下，Blinn模型更符合实验结果。

解释图源《Unity Shader入门精要》