Unity3d客户端面经准备

边敲边记，打起精神，屡败屡战

语言相关

面向对象语言的三大特性

继承、封装、多态

继承

继承可以使得子类具有父类的各种属性和方法，而不需要再次编写相同的代码。在令子类继承父类的同时，可以重新定义某些属性，并重写某些方法，即覆盖父类的原有属性和方法，使其获得与父类不同的功能。

封装

隐藏对象的属性和实现细节，仅对外公开接口，控制在程序中属性的读取和修改的访问级别。

多态

相同的消息可能会送给多个不同类别的对象，系统根据对象所属类别，引发对应类别的方法，而有不同的行为。

多态分为编译时多态和运行时多态，编译时多态也称为静态联编，通过重载和模板来实现，运行时多态称为动态联编，通过继承和虚函数来实现。

虚函数

虚函数(多态的实现方式)：当使用类的指针调用成员函数时，普通函数由指针类型决定，而虚函数由指针指向的实际类型决定。

虚函数表指针(vptr)会指向一张名为“虚函数表”的表(在堆中)，表中数据为函数指针，调用时通过对象内存找到对应虚函数的实现区域并调用。

构造函数不能是虚函数，而析构函数可以是虚函数且最好设置为虚函数(避免内存泄漏)。

new和malloc的区别

malloc和free是库函数，new和delete是C++操作符，new自己计算空间的大小，而malloc需要指定大小

C#装箱拆箱

装箱就是将值转换为引用类型，拆箱就是将引用类型转换为值类型

int i = 1;
object o = i; // 将整型变量i装箱分配给o

o = 2;
i = (int)o; // 将对象o拆箱分配给整型变量i

const修饰符的用法

const常用来定义一个常量，这个常量是不可变的，也就是一旦被定义后不可以对其进行修改。

常见的用法：const变量为只读，不应被改变，可以通过编译的错误提示来检查错误，提高程序的安全性和可靠性。

注意不能与static修饰符同时使用，如const static int value是错误的

指针常量和常量指针

指针常量：指针修饰的常量，该指针不能被修改，地址类的内容可以修改

int a, b;
int * const p = &a; // 指针常量
// 记忆技巧：指针(int *)常量(const)
*p = 9; // 成功
p = &b; // 失败

常量指针：定义指针变量时，数据类型前用const修饰，即指向常量的指针变量，指针指向的变量的值不可通过该指针修改，但指针指向的值可以改变（修改地址）
```
int a, b;
const int * p = &a; // 常量指针
// 记忆技巧：常量(const)指针(int *)
*p = 9; // 失败
p = &b; // 成功
```

static修饰符的用法

static是静态的，不变的，在某一个类中只有一个，不会因实例化对象的不同而不同。在声明一个类时使用static关键字，具有两个方面的意义：防止程序员在代码中实例化该静态类；防止在类的内部声明任何实例字段或方法

静态类的主要特性：

仅包含静态成员
无法实例化
静态类的本质，是一个抽象的密封类，所以不能被继承，也不能被实例化
不能包含实例构造函数
如果一个类下面的所有成员，都需要被共享，那么可以把这个类定义为静态类

一般在单例模式下被使用

内存泄漏

向系统申请分配内存进行使用，但是使用完没有释放内存。

以发生的方式分类，内存泄漏可以分为4类：

常发性内存泄漏：发生发生内存泄漏的代码被多次执行到，每次被执行的时候都会导致一块内存泄漏
偶发性内存泄漏：发生内存泄漏的代码只在某些特定环境或操作过程下才会发生。常发性和偶发性是相对的，对于特定环境，偶发性也许变成了常发性
一次性内存泄漏：发生内存泄漏的代码只会被执行一次，或者由于算法上的缺陷，导致总会有一块且仅一块内存发生泄漏。比如，在类的构造函数中分配内存，在析构函数中却没有释放该内存。
隐式内存泄漏。程序在运行过程中不停的分配内存，但是直到结束时才释放内存。严格来说没有发生内存泄漏，但是不及时释放内存也可能导致最终耗尽系统的内存，所以称为隐式内存泄漏

从用户使用程序的角度来看，内存泄漏本身不会产生什么危害，作为一般的用户，根本感觉不到内存泄漏的存在。真正有危害的是内存泄漏的堆积，这会最终消耗尽系统所有的内存。从这个角度来说，一次性内存泄漏并没有什么危害，因为它不会堆积，而隐式内存泄漏危害性则非常大，因为较之于常发性和偶发性内存泄漏它更难被检测到

智能指针

C++在STL中提供了四种智能指针：auto_ptr, unique_ptr, shared_ptr, weak_ptr，auto_ptr在C++98中提出，在C++11中被摒弃，并提出unique_ptr代替auto_ptr

unique_ptr

旨在替代不安全的auto_ptr。它持有对对象的独有权，两个unique_ptr不能指向一个对象，即unique_ptr不共享它所管理的对象。它无法复制到其他unique_ptr，无法通过值传递到函数，也无法通过值传递到函数，也无法用于需要副本的任何标准模板库算法。只能移动unique_ptr，即对资源管理权转移，并且原始unique_ptr不再拥有此资源

unique_ptr<int> ptrA(new int(1)); // 构建
unique_ptr<int> ptrB = std::move(ptrA); // 所有权转移
ptrB.reset(ptrA.release()); // 所有权转移

unique_ptr与原始指针一样有效，并可用于STL容器。

实现方式是将拷贝构造函数和赋值操作符都声明为delete或private

auto_ptr

与unique_ptr类似，但是允许拷贝，由于拷贝后原对象变得无效，再次访问原对象会导致程序崩溃(而unique_ptr则会在编译过程中报错)，在访问unique_ptr前，可以使用get()进行判空操作

unique_ptr<string> upt1 = std::move(upt);
if(upt.get() != nullptr)
{
    // do something
}

unique_ptr还扩展了auto_ptr的功能

可放在容器中

vector<unique_ptr<string>> vs{ new string("AA"), new string("BB") };

管理动态数组

unique_ptr<int[]> p (new int[3]{1,2,3});
p[0] = 0;

自定义资源删除操作

void end_connection(connection *p) {disconnect(*p);}

shared_ptr

引用计数放在堆上，多个shared_ptr的对象引用计数都指向同一个堆地址

实现手写

class Point{
private:
    int x, y;
public:
    Point(int xVal=0, int yVal=0) : x(xVal), y(yVal) {}
    int getX() const {return x;}
    int getY() const {return y;}
    void setX(int xVal) {x = xVal;}
    void setY(int yVal) {y = yVal;}
}

class RefPtr{
private:
    friend class SmartPtr;
    RefPtr(Point *ptr):p(ptr), count(1) {}
    ~RefPtr(){delete p;}

    int count;
    Point *p;
}


class SmartPtr{
private:
    RefPtr* rp;
public:
    // 构造函数
    SmartPtr() { rp = nullptr; }
    SmartPtr(Point* ptr) : rp(new RefPtr(ptr)) {}
    SmartPtr(const SmartPtr &sp) : rp(sp.rp) {
        rp->count += 1;
    }
    // 重载运算符
    SmartPtr& operator=(const SmartPtr& rhs) {
        rhs.rp->count += 1;
        if (rp != nullptr && --rp->count == 0)
        {
            delete rp;
        }
        rp = rhs.rp;
    }

    Point* operator->() {
        return rp->p;
    }

    Point& operator*() {
        return *(rp->p);
    }

    ~SmartPtr(){
        if(--rp->count == 0) delete rp;
        else cout << rp->count << "pointers left\n";
    }
}

智能指针的使用注意事项

优先使用make_shared和make_unique是为了避免内存泄漏

不使用相同的内置指针值初始化，或reset多个智能指针
不delete get()返回的指针
不使用get()初始化或reset另一个智能指针
get()返回的智能指针可能变成dangling pointer
如果智能指针管理的内存不是new出来的，需要提供删除器

算法与数据结构

红黑树

节点颜色有红色和黑色
根节点必为黑色
所有叶子节点都是黑色(空节点)
任意节点到叶子节点经过的黑色节点数节目相同
不会有连续的红色节点

排序算法

作为算法的第一课，大部分笔试也会对此进行涉及，所以还是要多加重视

冒泡排序

比较相邻的元素。如果第一个比第二个大，就交换他们两个。

对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

针对所有的元素重复以上的步骤，除了最后一个(因为已经是最大的了)。

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

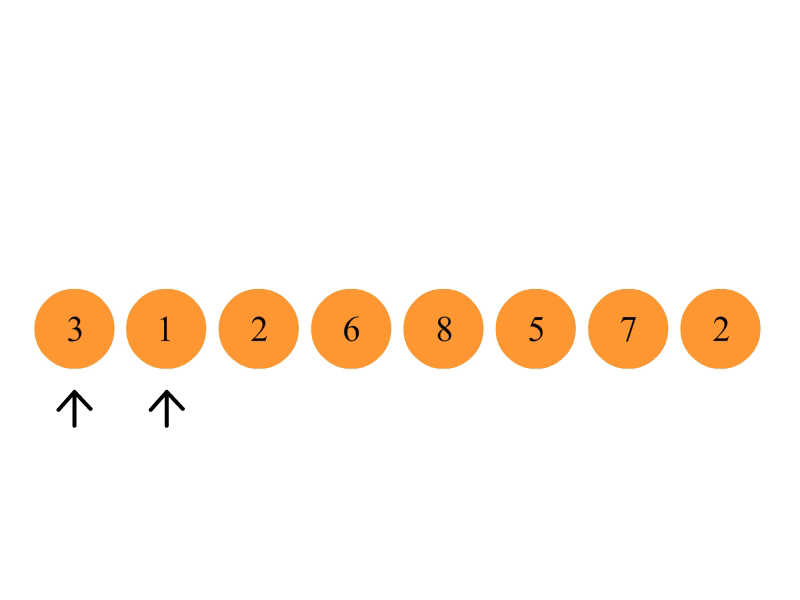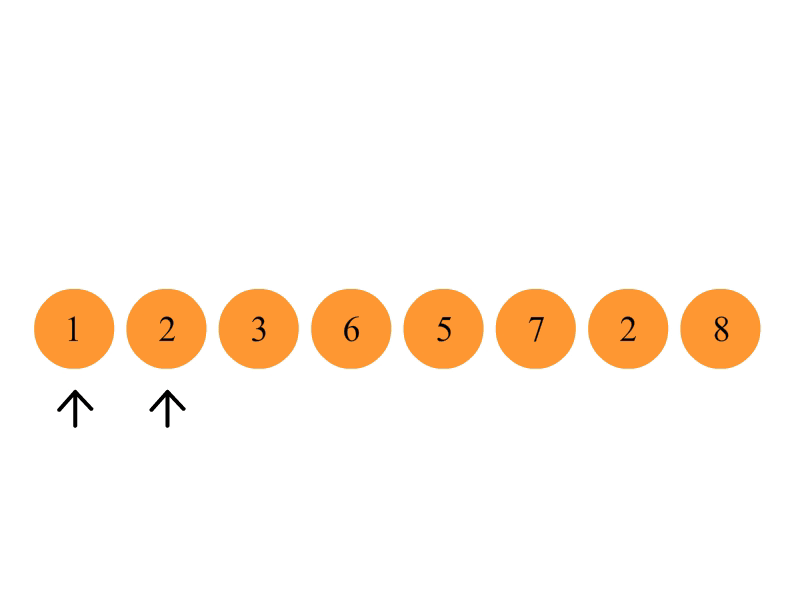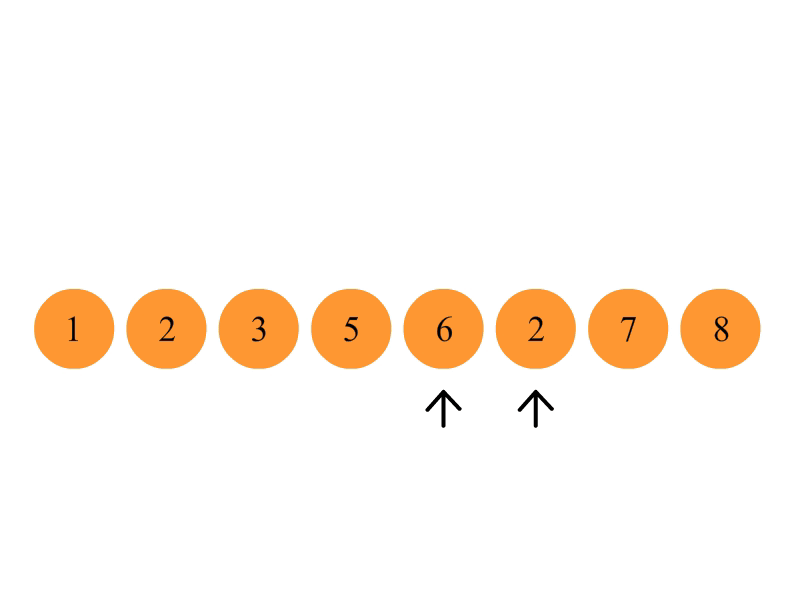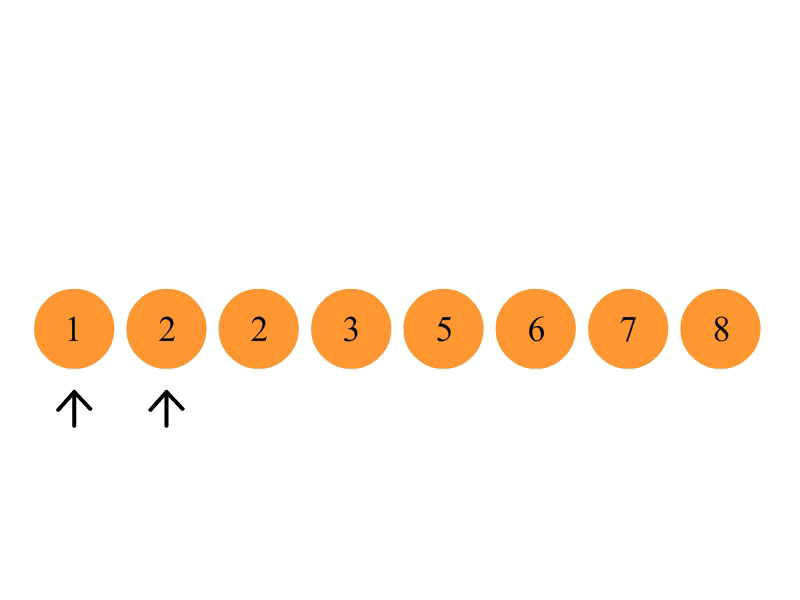
算法复杂度：

空间复杂度： $O(1)$
最坏时间复杂度： $O(n^2)$
最好时间复杂度： $O(n)$
平均时间复杂度： $O(n^2)$

void BubbleSort(int *num, int size)
{
    int i, j, tmp;
    for (i = 0; i < size - 1; i++)
    {
        for (j = 0; j < size - i - 1; j++)
        {
            if (num[j] > num[j + 1])
            {
                tmp = num[j];
                num[j] = num[j + 1];
                num[j + 1] = tmp;
            }
        }
    }
}

选择排序

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。

再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

重复第二步，直到所有元素均排序完毕。

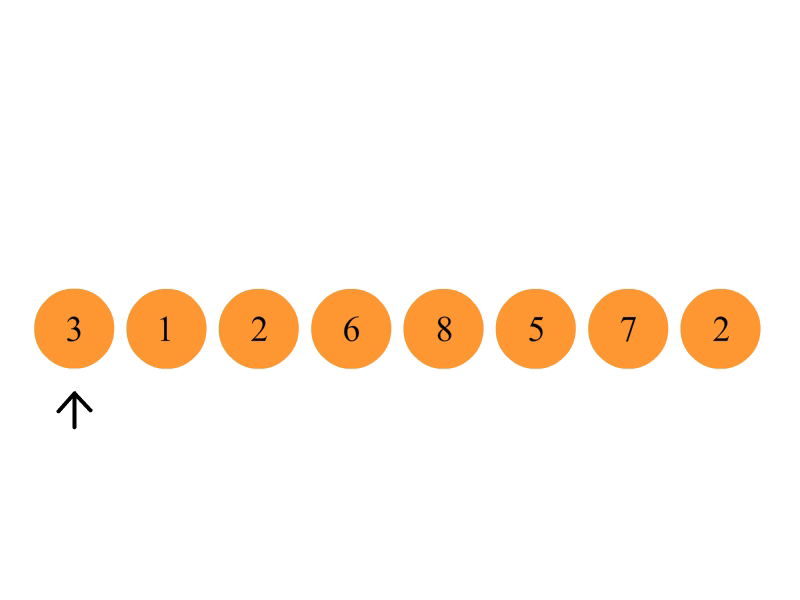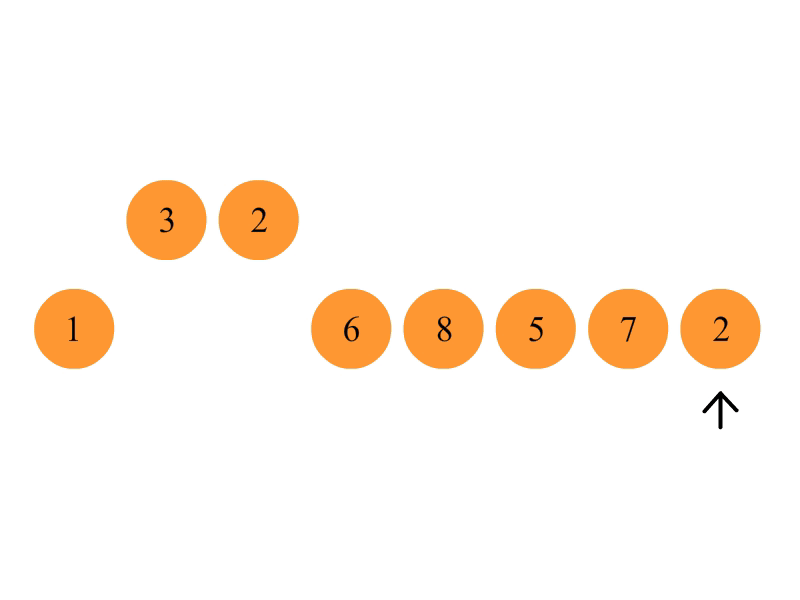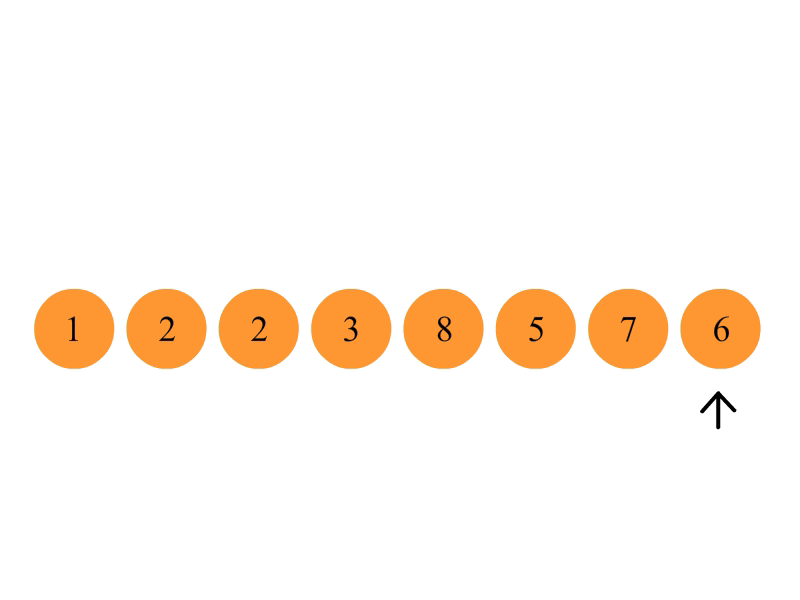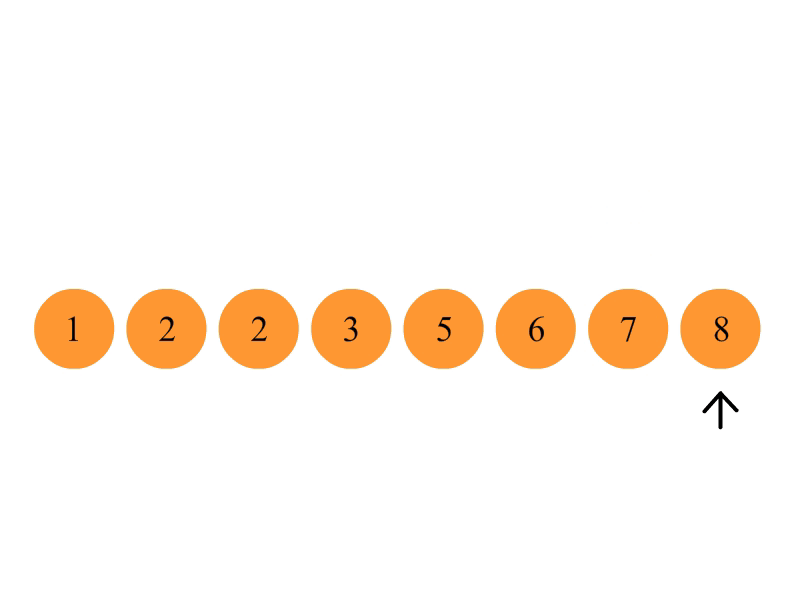
算法复杂度：

空间复杂度： $O(1)$
最坏时间复杂度： $O(n^2)$
最好时间复杂度： $O(n^2)$
平均时间复杂度： $O(n^2)$

void SelectionSort(int *num, int size)
{
    int min, minPos;
    for (int i = 0; i < size; i++)
    {
        min = num[i];
        minPos = i;
        for (int j = i + 1; j < size; j++)
        {
            if (num[j] < min)
            {
                minPos = j;
                min = num[j];
            }
        }
        num[minPos] = num[i];
        num[i] = min;
    }
}

插入排序

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

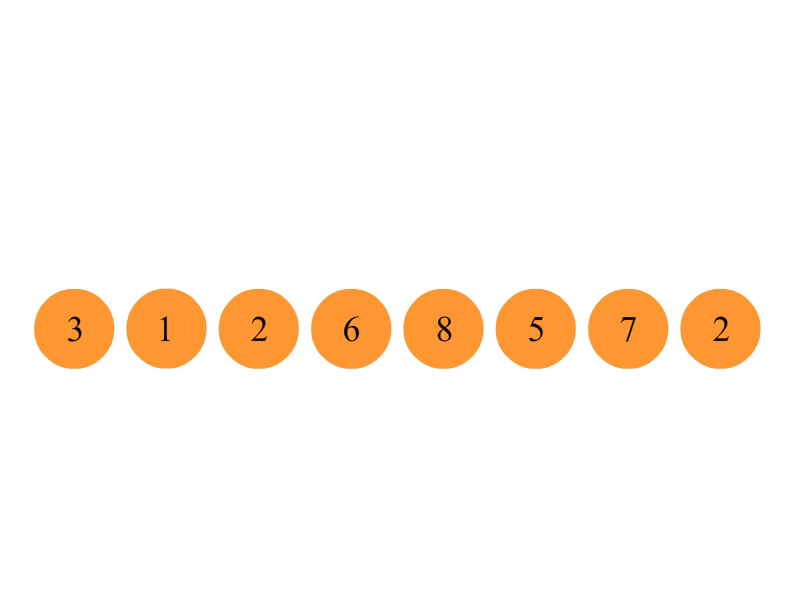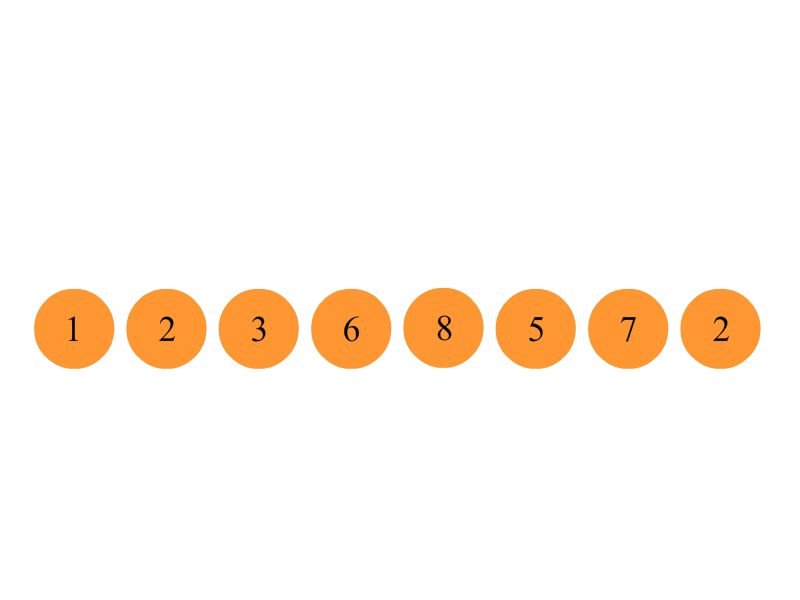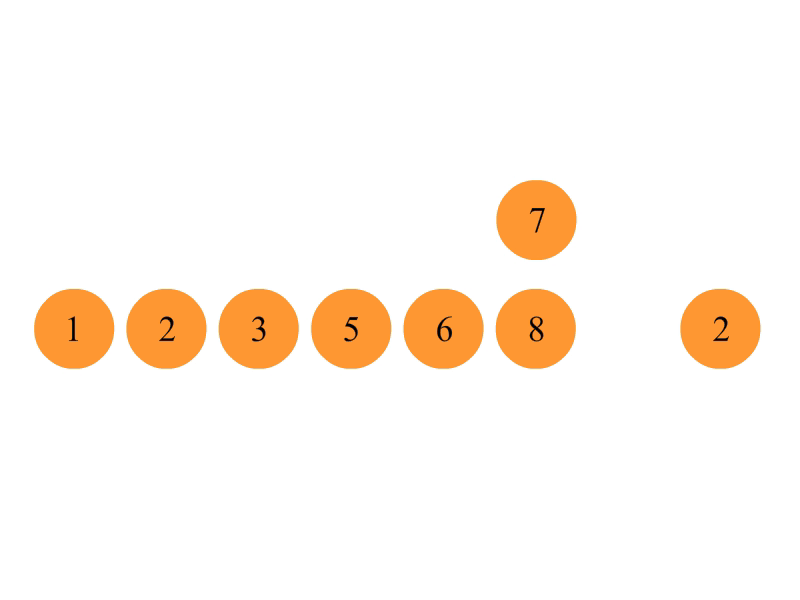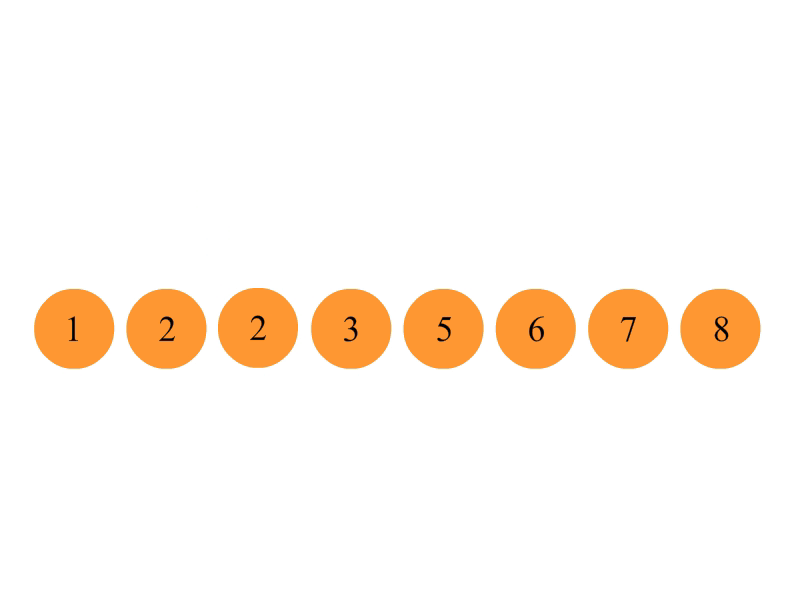
算法复杂度：

空间复杂度： $O(1)$
最坏时间复杂度： $O(n^2)$
最好时间复杂度： $O(n)$
平均时间复杂度： $O(n^2)$

void InsertSort(int *num, int size)
{
    int key, i, j;
    bool isDone;
    for (i = 1; i < size; i++)
    {
        key = num[i];
        isDone = false;
        for (j = i - 1; j >= 0; j--)
        {
            if (key < num[j])
            {
                num[j + 1] = num[j];
            }
            else
            {
                num[j + 1] = key;
                isDone = true;
                break;
            }
        }
        //处理当前数字是最小的情况
        if (!isDone)
            num[0] = key;
    }
}

归并排序

1.申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

2.设定两个指针，最初位置分别为两个已经排序序列的起始位置；

3.比较两个指针所指向的元素，选择相对小的元素放入到合并空间并移动指针到下一位置；

4.重复步骤 3 直到某一指针达到序列尾；

5.将另一序列剩下的所有元素直接复制到合并序列尾。

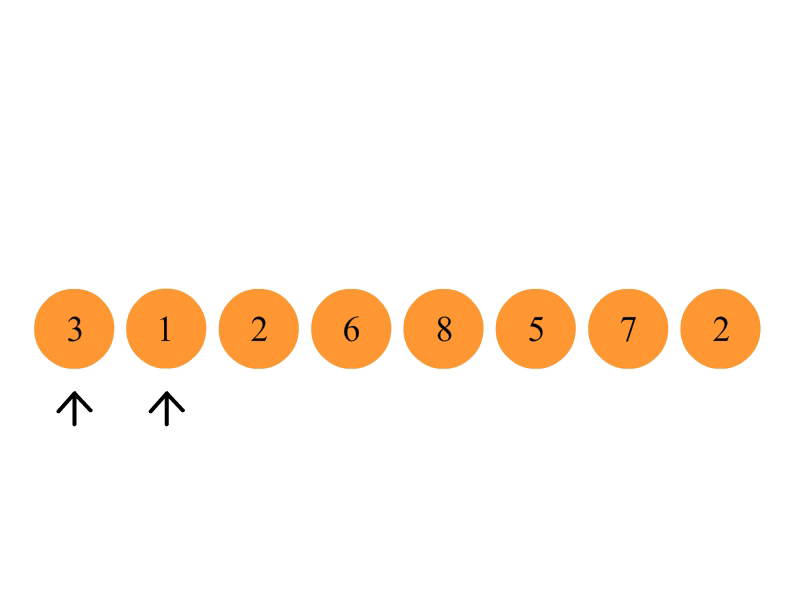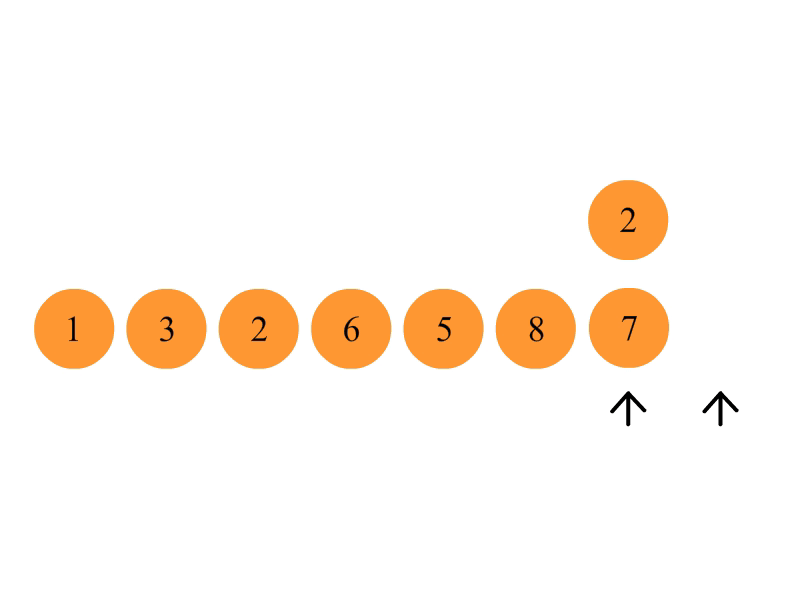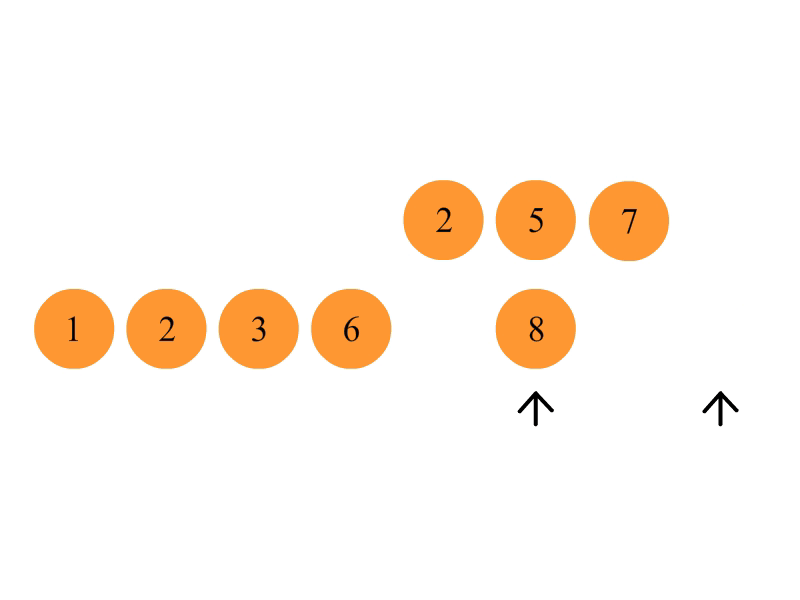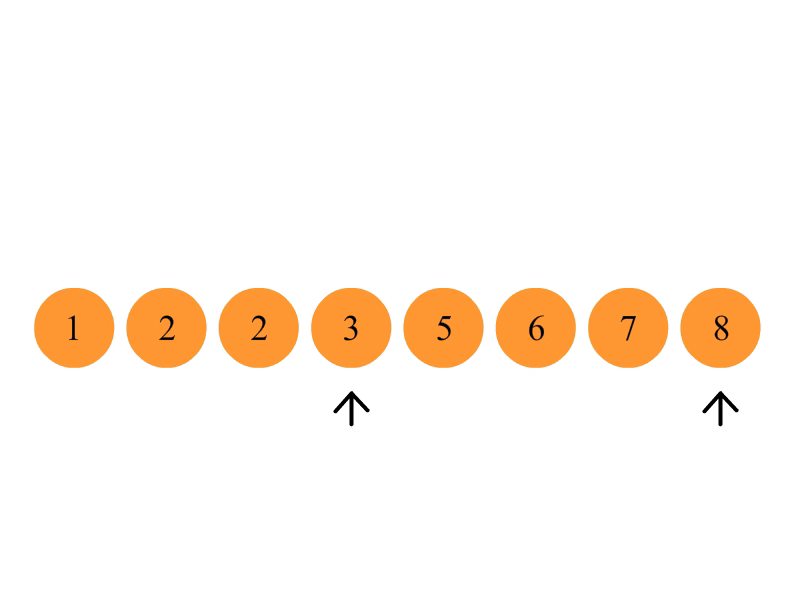
算法复杂度：

空间复杂度： $O(n)$
最坏时间复杂度： $O(n\lg n)$
最好时间复杂度： $O(n\lg n)$
平均时间复杂度： $O(n\lg n)$

void MergeSort(int num[], int size)
{
    int len, start, end; // len为已有序数组的长度
    for (len = 1; len < size; len *= 2)
    {
        for (start = 0, end = start + len * 2 - 1; start < size; start += len * 2, end += len * 2)
        {
            int *left = new int[len];
            int *right = new int[len];
            int rightlen = 0, leftlen = 0;
            // 拷贝数据进左右队列
            for (int i = 0; i < len && start + i < size; i++)
            {
                left[i] = num[start + i];
                leftlen++;
            }
            for (int i = 0; i < len && start + len + i < size; i++)
            {
                right[i] = num[start + len + i];
                rightlen++;
            }

            int i = 0, j = 0;
            for (int index = start; index < start + len * 2 && index < size; index++)
            {
                // 左或右队列已全部放入
                if (i >= leftlen)
                {
                    num[index] = right[j];
                    j++;
                }
                else if (j >= rightlen)
                {
                    num[index] = left[i];
                    i++;
                }
                // 比较左右队列的当前数字，小的放入
                else if (left[i] <= right[j] || j >= rightlen)
                {
                    num[index] = left[i];
                    i++;
                }
                else
                {
                    num[index] = right[j];
                    j++;
                }
            }

            delete[] left;
            delete[] right;
        }
    }
}

快速排序

从数列中挑出一个元素，称为 “基准”（pivot）;

重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

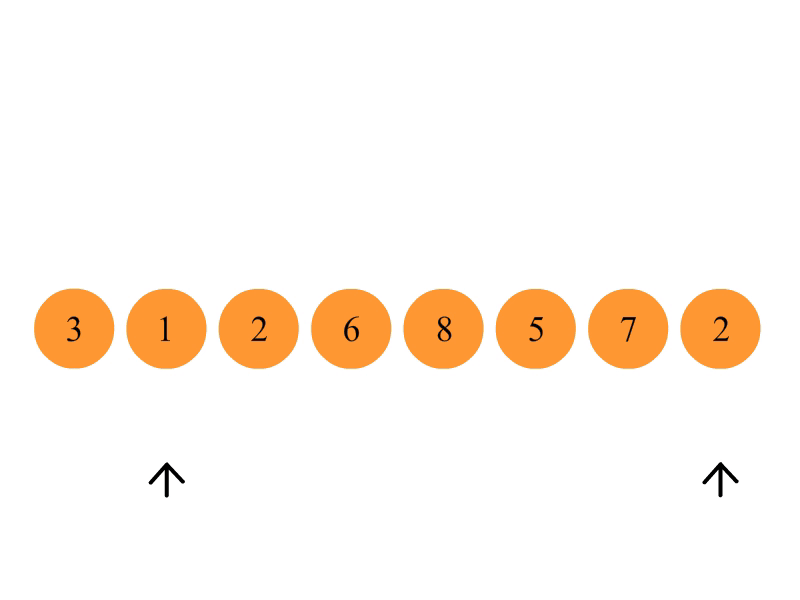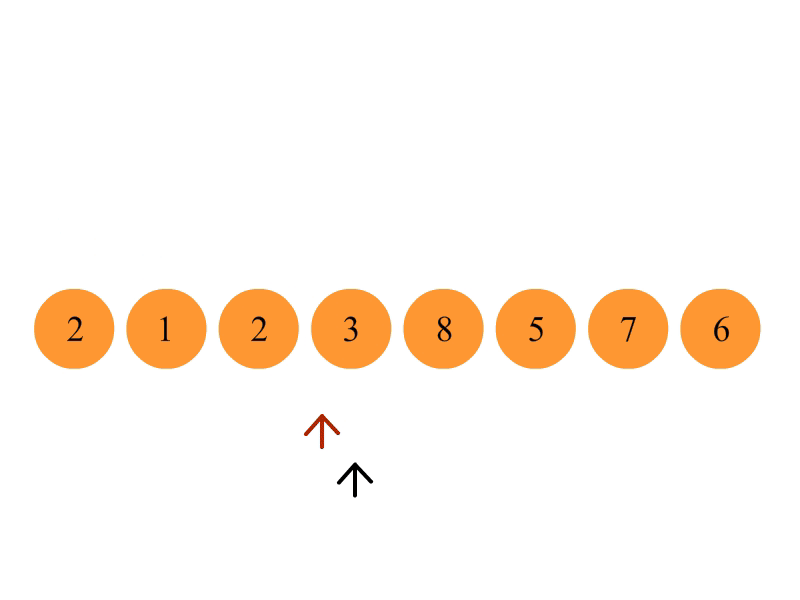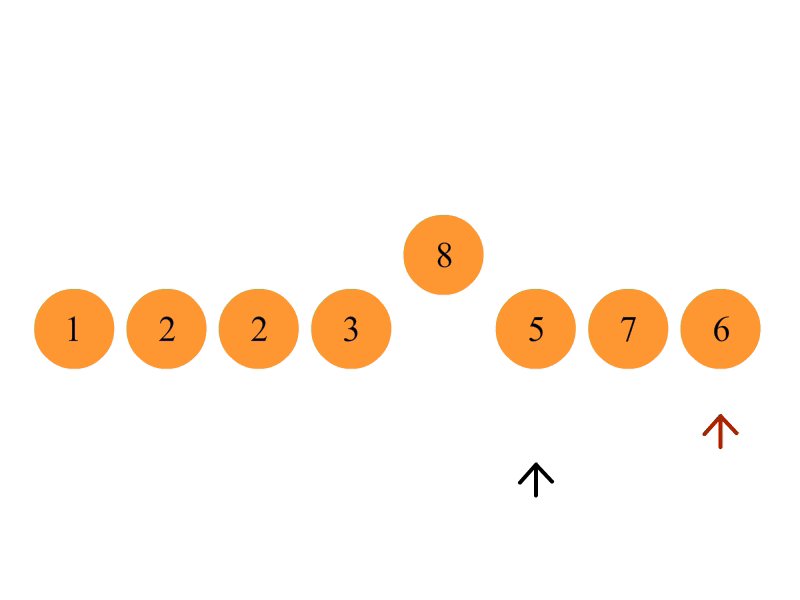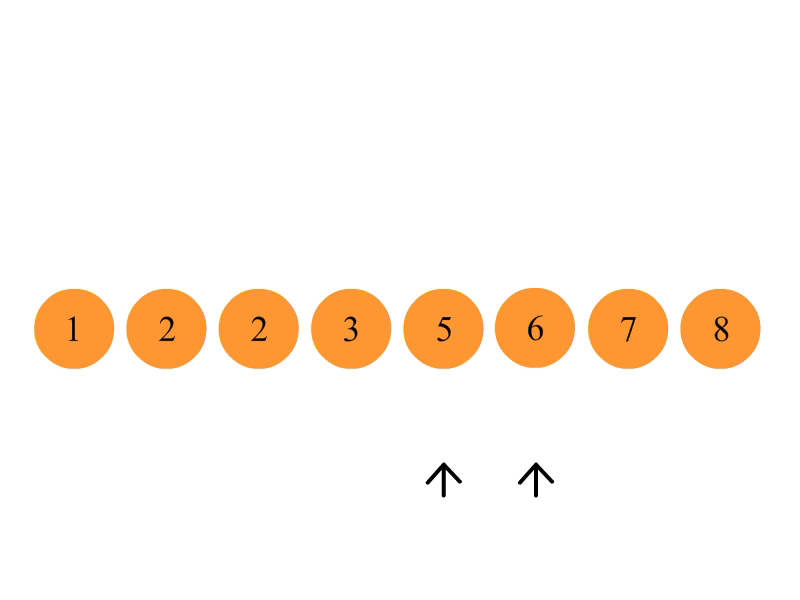
算法复杂度：

空间复杂度： $O( \lg n)$
最坏时间复杂度： $O(n^2)$
最好时间复杂度： $O(n \lg n)$
平均时间复杂度： $O(n\lg n)$

#include <stack>
using namespace std;

class Seg
{
public:
    int start, end;
    Seg(int _start, int _end)
    {
        start = _start;
        end = _end;
    }
};

void QuickSort(int *num, int size)
{
    stack<Seg> st;
    Seg firstSeg(0, size - 1);
    st.push(firstSeg);

    while (st.size() > 0)
    {
        int start, end, pivot;
        Seg seg = st.top();
        st.pop();
        start = seg.start, end = seg.end;
        pivot = start;

        bool isDone = false;
        int left, right, key;
        left = pivot + 1, right = end, key = num[pivot];
        while (left <= right)
        {
            isDone = false;
            while (num[right] >= key)
            {
                right--;
                if (right <= pivot)
                {
                    isDone = true;
                    break;
                }
            }
            if (isDone)
                break;
            num[pivot] = num[right];
            pivot = right;
            while (num[left] <= key)
            {
                left++;
                if (left >= pivot)
                {
                    isDone = true;
                    break;
                }
            }
            if (isDone)
                break;
            num[pivot] = num[left];
            pivot = left;
        }
        num[pivot] = key;

        if (start < pivot - 1)
        {
            Seg leftSeg(start, pivot - 1);
            st.push(leftSeg);
        }
        if (end > pivot + 1)
        {
            Seg rightSeg(pivot + 1, end);
            st.push(rightSeg);
        }
    }
}

堆排(TopK)

TopK问题描述：快速在一个无序序列中找到最大/最小的k个元素

最大k个：小顶堆；最小k个：大顶堆

小顶堆：

#include <vector>
#include <queue>
using namespace std;

void TopK(int *num, int size)
{
    priority_queue<int, vector<int>, greater<int>> q; // 大顶堆用less

    for(int i=0;i<size;i++)
    {
        if(q.size()>=10)
        {
            if(q.top()<num[i])
            {
                q.pop();
                q.push(num[i]);
            }
        }
        else
        {
            q.push(num[i]);
        }
    }

    for(int i = 0; i < 10;i++)
    {
        num[size-i-1] = q.top();
        q.pop();
    }
}

Unity

Unity的脚本生命周期

参考事件函数的执行顺序 - Unity 手册，抽取了比较重要的部分

加载第一个场景时

场景开始时调用以下函数，为场景中的每个对象调用一次：

Awake：始终在Start函数前并在实例化后调用此函数(每次激活也会调用)
OnEnable：在启用对象后立即调用此函数，创建示例时也会执行调用(仅在对象处于激活状态时调用)

Editor

不在游戏过程中，在编辑器下

Reset：使用Reset命令可以初始化脚本的属性(即将脚本附加到对象时，设定属性参数)

在第一次帧更新之前

Start：仅当启用脚本示例后，才会在第一次帧更新之前调用Start

帧之间

OnApplicationPause：允许发出一个额外帧来显示图形指示暂停状态

更新顺序

FixedUpdate：进行所有物理计算和更新，应用物理无需乘以Time.deltaTime，因为其调用基于可靠的计时器，独立于帧率
Update：没帧调用一次Update。用于帧更新的主要函数
LateUpdate：在Update完成后执行，一般用于摄像机的移动和旋转计算，确保角色在摄像机跟踪位置前已完全移动

销毁对象时

OnDestroy：对象存在的最后一帧完成所有帧更新之后，调用此函数

渲染管线

应用阶段

准备好场景数据，粗粒度剔除(culling)，将数据加载到显存
渲染图元，设置好每个模型的渲染状态
调用DrawCall

几何阶段

顶点着色器：坐标变换，逐顶点光照(输出顶点颜色)
裁剪：根据相机的角度以及配置(如裁剪图元的正面或背面)进行裁剪
屏幕映射：不可编程，将每个图元的xy坐标转换到屏幕座标系

光栅化阶段

三角形设置：计算三角网格表示数据的过程
三角形遍历：检查像素是否被一个三角网格所覆盖，如果被覆盖就生成一个片元(并不是真正意义上的像素，而是多种状态的集合，这些状态用于计算每个像素的最终颜色)
片元着色器：输入为对顶点着色器输出数据的插值得到的结果，输出为一个或多个的颜色值。
逐片元操作：解决片元的可见性，通过所有测试才写入颜色缓冲区。

UI合批

UGUI中Canvas可以嵌套子Canvas，合批是以Canvas为单位的。

合批的基本条件是两个控件使用的材质球(shader)和贴图要完全相同。

方法：使用图集(Editor->Project Setting->Editor下Sprite Packer选择Always Enable，右键Create->Sprite Atlas创建图集)

合批

要求相同的材质

静态合批

静态合批是将静态(不移动)GameObjects组合成大网格，然后进行绘制，静态合批需要额外的内存来存储合并的几何体。

动态合批

动态合批是将一些足够小的网格，在CPU上转换它们的顶点，将许多顶点组合在一起并一次性绘制。

动态合批有节点数的限制(不超过900个顶点和不超过300个顶点的网格)。

不同材质的阴影会动态合批，只要绘制阴影的pass是相同的，因为阴影和其他贴图等数据无关。

GPU Instancing（更深入的话）

GPU Instancing可以使用一个DrawCall渲染多个相同网格的物体，不过也有一些其他的约束：

SRP下使用可以GPU instance可以用Graphics.DrawMeshInstanced
SkinnedMeshRenderers不支持GPU Instancing

图形学

三维空间变换（MVP）

待补充

Model Transform

控制物体的位置，旋转，缩放

View Transform

照相机的状态

Projection Transform

投影矩阵，一般的有正交投影和透视投影

设计模式（现在经常不考）

面向对象设计原则

单一职责原则

一个类只负责一个功能领域中的相应职责。或者说，一个类，最好只做一件事，只有一个引起它变化的原因。

开闭原则

一个软件实体应当对拓展开放，对修改关闭。即软件实体应尽量在不修改原有代码的情况下进行拓展。

里氏替换原则

所有引用基类（父类）的地方必须能透明的使用其子类的对象，并且保证原来程序的逻辑行为不变以及正确性不被破坏。

里氏替换原则是实现开闭原则的重要方式之一。将父类设计为抽象类或接口，让子类继承父类或实现父接口，并实现在父类中声明的方法，运行时子类示例替换父类示例，可以很方便扩展系统的功能，无须修改原有子类的代码，增加新的功能可以通过增加新的子类来实现。

依赖倒置原则

抽象不应该依赖于细节，细节应当依赖于抽象。换句话说，要针对接口编程，而不是针对实现编程。

接口隔离原则

使用多个专门的接口，而不使用单一的总接口，即客户端不应该依赖那些他不需要的接口。

合成复用原则

尽量使用对象组合，而不是继承来达到复用的目的。

迪米特法则

一个软件实体应当尽可能少地与其他实体发生相互作用。

工厂模式

定义一个创建对象的接口，让其子类自己决定实例化哪一个工厂类，工厂模式使其创建过程延迟到子类进行。这满足创建型模式中所要求的“创建与使用相分离”的特点。

例：技能作为一系列类，可以使用工厂模式创建

观察者模式

观察者模式定义了对象间的一对多关系，当一个对象状态发生变化，所有依赖于它的对象都将得到通知并自动更新。

发布-订阅者模式

是一种消息范式，消息的发送者(发布者)不会将消息直接发送给特定的接收者(订阅者)，而是将消息分为不同的类别，无需了解哪些订阅者可能存在。同样的，订阅者可以表达对一个或多个类别的兴趣，只接收感兴趣的消息，无需了解哪些发布者存在。

单例模式

在C#应用中，单例对象能保证在一个CLR中，该对象只有一个实例存在。而且自行实例化并向整个系统提供这个实例，避免频繁创建对象，节约内存。

public class Singleton
{
    private static Singleton instance;
    private Singleton(){}
    public static Singleton getInstance()
    {
        if(instance == null)
        {
            instance = new Singleton();
        }
        return instance;
    }
}

饿汉模式

在类加载的时候立刻实例化，后续使用只出现一份实例

懒汉模式

在调用实例方法的时候再进行实例化，在不想使用时不会实例化

饱汉模式

直接new出来

代理模式

一个是真正的你要访问的对象，一个是代理对象，真正对象与代理对象实现同一个接口，先访问代理类再访问真正要访问的对象。

多用于代理text，button等组件，以及委托

命令模式

一种以数据驱动的设计模式，属于行为型模式。请求以命令的形式包裹在对象中并传给调用对象。调用对象寻找可以处理该命令的合适的对象，并把命令传给相应的对象，该对象执行命令。

命令模式将“请求”封装成对象，以便使用不同的请求，队列或日志来参数化其他对象，同时支持可撤销的操作。